PROYECTOS DE CIENCIAS: CATAPULTA DE DA VINCI

Trabajo presentado por:

•CASTRO BRICEÑO Víctor André

•CORRO AGUIRRE Kiara Alessandra

•PASACHE LAGUNA Max Junior

•PINEDO SOLANO Jan Carlos

•TERRONES RAMOS Miguel Orlando

Revisado por: Elvis Hermes Malaber

..................................................................................................................................................................

INTRODUCCIÓN

Debido a los avances de la ciencia y la tecnología es probable que nos encontremos con fenómenos físicos que ocurran en ámbitos especiales, como puede ser aquellos que toman lugar a mucha distancia de nuestro alcance (espacio exterior) o en lugares de dimensiones reducidas (interior del cuerpo humano). Dado que estamos limitados por nuestros sentidos, en especial la vista, recurrimos a distintas herramientas, tales como microscopios, telescopios, etc., para presenciar dichos fenómenos físicos, y aun así el estudio de los mismos es complicado.

En nuestro presente informe queremos dar a conocer nuestro proyecto de física, el cual consiste en utilizar una catapulta para demostrar diferentes leyes físicas.

La catapulta, un instrumento militar utilizado en la antigüedad para el lanzamiento a distancia de grandes objetos (en nuestro caso una canica) a modo de proyectiles. Fue inventada probablemente por los griegos y posteriormente mejorada por los cartagineses y romanos, siendo muy empleada en la Edad Media.

Las catapultas son perfectas para explicar los movimientos parabólicos, estas lanzan proyectiles con un ángulo con la horizontal, con una velocidad inicial o velocidad en X que siempre es constante, el proyectil también tiene una velocidad en Y que es independiente a la velocidad en X, el cuerpo tiene una altura máxima, un alcance máximo y un tiempo de vuelo.

Tiene un funcionamiento en el que primero se llega al almacenamiento de la energía potencial. La máquina, para transmitir esa energía almacenada al proyectil, necesita gastar parte de esa energía almacenada (moviendo del brazo de palanca, desplazamiento de la honda, rozamiento de cuerdas, etc.); así, el proyectil recibe la energía potencial que no ha sido gastada por la catapulta y sale disparado, con una energía denominada energía cinética

la cual es la energía de un objeto cuando se desplaza, de la cual dependerá la distancia que alcance y su tiempo de vuelo.

OBJETIVOS

- Diseñar una catapulta de Da Vinci para aplicar los conocimientos adquiridos en el curso de Física.

FUNDAMENTO TEÓRICO

I. CATAPULTA

1.1 HISTORIA

Una catapulta es un instrumento militar utilizado en la antigüedad para el lanzamiento a distancia de grandes objetos a modo de proyectiles. Fue inventada probablemente por los griegos y posteriormente mejorada por los cartagineses y romanos, siendo muy empleada en la Edad Media.

Los ingenieros que trabajaban para Dionisio de Siracusa desarrollaron las primeras catapultas basándose en los arcos de la época, fue la primera máquina militar en la cual se utilizó la fuerza de gravedad y la caída de pesos, para impartir la energía necesaria a un proyectil. Para los antiguos ingenieros problema fue que, a medida que el tamaño del arco se hace más grande, el esfuerzo para poder tensarlo aumenta considerablemente disminuyendo su manejabilidad, la solución fue suplir la fuerza humana por ingenieros mecánicos estableciéndose así una tradición de manipulación mecánica que llega hasta nuestros días.

Las catapultas permitían lanzar proyectiles de 40 a 100 kg a 300 o 400 m de distancia. Estas máquinas almacenan energía para liberarla en un disparo, mediante el siguiente proceso:

· Almacenamos una energía en la catapulta, llamada energía potencial (EP).

· La máquina, para transmitir esa energía almacenada al proyectil, necesita gastar parte de esa energía almacenada (movimiento del brazo de palanca, desplazamiento de la honda, rozamiento de las cuerdas, etc.).

· El proyectil recibe la energía potencial que no ha sido gastada por la catapulta y sale disparado, con una energía denominada energía cinética (EC), energía de un objeto que se desplaza), de la cual dependerá la distancia que alcance y su tiempo de vuelo.

1.2 CLASIFICACIÓN

2.2.1 Catapulta de tensión: Son las que funcionan gracias a que almacenan su energía, al ser tensado un arco de metal, madera o cuero y fueron las primeras en hacer su aparición, ya que descienden directamente de los arcos manuales. Algunas catapultas de asalto romanas utilizaban este sistema desde el primer ciclo antes de Cristo, con algunas variantes.

2.2.2 Catapulta de torsión: Son aquellas que son accionadas gracias a la fuerza almacenada al “torcer”, una madeja de cuerdas, tendones o crin de caballo, según la época de que se trate. Algunos ejemplos de este tipo son: las Ballestas, los Onagros, el escorpión, etc.

2.2.3 Catapulta de contrapeso: Fue un invento aparentemente reciente; por lo menos eso dicen algunos autores, sin embargo no todos coinciden en ello. Esta catapulta funcionaba a base de un contrapeso, con una masa muy superior al peso del proyectil, en el caso del Trebuchet con una relación que variaba de 80 a 100 veces. La ventaja de este tipo de máquina de guerra, con respecto a las anteriores, es que podía almacenar energía sin cambios ni fugas. Cosa que las anteriores, no podían ya que con el tiempo iban perdiendo su fuerza y elasticidad, incluso dañarse si no eran disparadas en un corto periodo de tiempo.

2.2.4 Catapulta de tracción: Fue un invento de los chinos que llamaron hsuan feng, utilizada aproximadamente en el año 200 de nuestra era. Esta catapulta funciona a base del impulso humano y su principio es muy parecido al del Trebuchet; es decir, utilizan la palanca y la honda para aumentar la fuerza de salida del proyectil. Esta catapulta fue sin duda el antepasado de Trebuchet, ya que es natural su evolución.

II. LEONARDO DA VINCI

2.1 BIOGRAFÍA

Nació el 15 de abril de 1452 en Anchiano, una aldea cerca de la ciudad de vinci en el valle del Arno, dentro de los territorios de Florencia, Italia. Aunque para otros nació en Vinci, de ahí su apellido, antes de que se adoptaran las convenciones de nombres actualmente vigentes en Europa, por lo que a su nombre de pila se añadió el de su padre Ser Piero y la localidad de nacimiento siendo entonces Leonardo di Ser Piero da Vinci. Sin embargo, Leonardo acostumbraba firmar sus trabajos como Leonardo o lo, Leonardo, yo Leonardo, es decir, sin emplear el nombre de su padre, lo que induce a pensar que era hijo ilegítimo. Era hijo natural de una campesina, Caterina (que se casó poco después con un artesano de la región), y de Ser Piero, un rico notario florentino.

Uno de los mayores genios que jamás ha dado la humanidad, evoca inmediatamente a la Gioconda, La última cena o El hombre de Vitruvio. Su labor artística no es solo más que la pequeña punta del iceberg de todos los conocimientos que consiguió reunir en torno a sí el genio italiano. Sin embargo, las ciencias fueron sin duda, una de las cosas en las que más se expandió, ya fuera en anatomía, ingeniería, botánica, biología o geometría. Su método de aprendizaje era simple: observación de la naturaleza y experimentación. De hecho, sus orígenes estuvieron más bien alejados de los manuales y las bibliotecas. Lo prueba el hecho de que hasta una edad ya adulta no aprendió latín, idioma dominante en la ciencia del siglo XVI. “Soy plenamente consciente de que al no ser un hombre de letras, ciertas personas presuntuosas puedan pensar que tienen motivos para reprochar mi falta de conocimientos. ¡Necios! Acaso no saben que puedo contestarles con las palabras que Mario dijo a los patricios romanos: Aquéllos que se engalanan con las obras ajenas nunca me permitirán usar las propias”, escribió al respecto dolido con aquellos que minusvaloraron su obra.

2.2 APORTACIONES A LA HUMANIDAD DE DA VINCI

2.2.1 Vehículo autopropulsado: Considerado en la actualidad como el primer automóvil del que se tuvo constancia. Leonardo da Vinci ideó el invento en madera, y funcionaba gracias a un mecanismo que provocaba la interacción de muelles con unas ruedas dentadas. Durante el año 2004, un grupo de científicos decidió recrear el invento. La reconstrucción fue tan exitosa que el aparato funcionaba exactamente como el inventor había pretendido muchos años antes.

2.2.2 Tornillo aéreo: Siguiendo con su faceta de inventor, da Vinci ideó el primer boceto del mecanismo que permitiría el funcionamiento de los helicópteros. El científico basó su teoría en la idea de que, igual que hace un tornillo, si hay un objeto “atornillándose” en el interior de un cuerpo sólido, la lógica conduce a pensar que éste deberá elevarse hacia arriba automáticamente. El inventor llamó a esta teoría “tornillo aéreo”.

2.2.3 La escafandra: Una de las obsesiones más conocidas del inventor era el mar. La posibilidad de explorarlo de forma cercana le condujo a idear diversos inventos para facilitar la tarea. Leonardo da Vinci diseñó un traje de buzo realizado en cuero, que se conectaba a una manga de aire, fabricada en caña. A su vez, ésta se conectaba a una campana que flotaba en la superficie. El científico tuvo en cuenta todos los detalles, y diseñó una bolsa en la que poder orinar durante la exploración.

2.2.4 Los engranes: Arquímedes ya había inventado con anterioridad la rueda dentada. Sin embargo, fue da Vinci el que creó los engranajes en todas sus formas. Dejó por escrito los esquemas y dibujos de muchos de los engranajes que se siguen empleando en la actualidad. El engranaje básico del que parten los demás consiste en una pareja de ruedas, una de ellas provista de barras cilíndricas. La otra se forma a su vez por dos ruedas unidas también por barras cilíndricas.

2.2.5 El hombre de Vitruvio: A partir de la información aportada por Vitruvio en lo referente a las proporciones, da Vinci modeló la forma humana perfecta. Como buen humanista, Leonardo da Vinci se encontraba embaucado por el hombre como microcosmos; hecho que le condujo a investigar en este campo.

2.2.6 La anatomía: En consonancia con el punto anterior, da Vinci dedicó parte de su trabajo al estudio de la anatomía humana. El científico estaba completamente fascinado por el cuerpo humano, y ello le llevó a conocerlo bien de cerca. En aquella época, tales investigaciones estaban fuertemente penadas con castigos que frecuentemente implicaban la muerte.

2.2.7 Tras la tragedia que arrasó la ciudad de Milán con la enfermedad de la peste, Leonardo da Vinci se propuso diseñar a través de bocetos la perfecta ciudad. Explotando su faceta de arquitecto urbanista, el científico renacentista planteó una ciudad repleta de zonas saneadas y canalización de agua. En lo referente a la higiene, da Vinci había diseñado la ciudad ideal, capaz de atajar una crisis como la sufrida con la peste anteriormente y evitar así nuevas catástrofes de mortalidad.

2.2.8 Las eras geológicas: Da Vinci se preocupó también de conocer aspectos de la geografía. En la época en la que el científico y artista vivió, se creía fervientemente que aquellos moluscos que aparecían en la cima de las montañas se debían al gran Diluvio Universal. Sin embargo, él se planteó que aquellas montañas, en algún momento anterior, podían haberse encontrado debajo de la línea del mar, y que posteriormente se desplazaron. Se dio paso así a la posterior investigación geológica.

2.2.9 Catapulta: Leonardo se interesó por casi todos los problemas mecánicos y cinemáticos de su época, como la caída libre de los cuerpos, el funcionamiento de las palancas y de las poleas, y la trasmisión de esfuerzos por medio de engranajes y otros sistemas. Uno de sus grandes aportaciones fue esta.

III. CATAPULTA DE DA VINCI

Máquina que puede lanzar piedras (en este caso algún proyectil pequeño), pueden colocarse en la catapulta y ser lanzados a grandes distancias. Esta máquina mejorada de Da Vinci fue pensado para la guerra.

IV. RELACIÓN DE LA CATAPULTA DE DA VINCI CON LA FÍSICA

Para analizar la catapulta hay que partir de la base que en su funcionamiento ocurre conservación de la energía, es decir la energía potencial existente en el momento en que el contrapeso se encuentra suspendido en el aire se transformará en energía cinética al momento en que el proyectil abandone la catapulta.

Para poder entender el funcionamiento de la catapulta, también hay que analizar los efectos físicos que en ella actúan, es por eso que antes de entrar de lleno en las fórmulas físicas que rigen a la catapulta, a continuación definiremos uno de estos efectos para que así se haga más fácil comprender el accionar de esta catapulta.

4.1 MOVIMIENTO PARABÓLICO

El movimiento parabólico es el movimiento de una partícula o cuerpo rígido describiendo su trayectoria una parábola. Por ejemplo, el balón de fútbol cuando es chutado por un jugador y cae al suelo es un movimiento parabólico.

Se puede analizar como la unión de dos movimientos. Por un lado, la trayectoria en la proyección del eje de las x (el eje que va paralelo al suelo) describirá un movimiento rectilíneo uniforme. Por otro lado, la trayectoria de la partícula al elevarse o caer verticalmente (en proyección sobre el eje de las y) describirá un movimiento rectilíneo uniformemente acelerado, donde la aceleración es la gravedad.

Para hacernos una idea visual de los dos componentes del movimiento parabólico, imaginemos un lanzamiento de peso de atletismo.

Si pudiésemos seguir el recorrido de la bola verticalmente desde arriba, en el mismo plano vertical de la trayectoria, desde esa posición privilegiada veríamos la bola avanzar a una velocidad constante, desde la salida de la mano del atleta hasta que la bola toca el césped. Apreciaríamos un movimiento rectilíneo uniforme (velocidad constante).

Pero si nos pudiésemos situar sobre el césped, detrás de donde se ubican los jueces y que estuviésemos también justo en el plano vertical de la trayectoria (es decir, que lanzase hacia nosotros) nos daría la impresión de que la bola sube y baja como si se tratase de un lanzamiento vertical hacia arriba (movimiento rectilíneo uniformemente acelerado).

4.1.1 TIPOS DE MOVIMIENTO PARABÓLICO

Existen diferentes tipos de movimiento parabólico dependiendo desde donde empieza o acaba el movimiento del cuerpo. Por ejemplo:

4.1.1.1 Movimiento parabólico completo: el cuerpo recorre una parábola completa, empezando y acabando en el suelo.

4.1.1.2 Movimiento de media parábola: el cuerpo empieza el movimiento desde cierta altura y es lanzado parabólicamente con una fuerza horizontal, en un punto que sería el punto más alto de la parábola completa ideal.

4.1.1.3 Otros movimientos parabólicos: existen muchos casos particulares del movimiento parabólico, por ejemplo el lanzamiento de una pelota desde el suelo a la terraza de una casa o el lanzamiento a canasta de un jugador de baloncesto. Siempre son tramos de una teórica parábola completa.


	Todos los elementos de los movimientos parabólicos se pueden calcular a partir del movimiento parabólico completo.

4.1.1 4.1.2 VELOCIDAD: La velocidad inicial del cuerpo ( Vo) tiene dos componentes, la componente horizontal, en el eje x y la componente vertical, en el eje vertical y. Depende de la fuerza con la que salga la partícula y el ángulo de lanzamiento.

La componente horizontal de la velocidad x será constante, ya que es un movimiento uniforme.

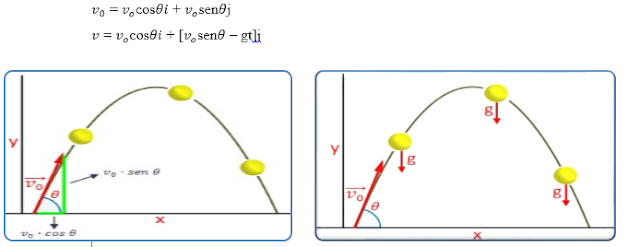
La componente vertical de la velocidad y disminuye inicialmente por la gravedad, hasta hacerse nula en el punto más alto de la trayectoria. A partir de ese punto, vuelve a crecer uniformemente acelerada por la gravedad. La fórmula de la velocidad es:

4.1.1 4.1.3 ACELERACIÓN: La aceleración solamente está presente en la componente vertical. El movimiento horizontal es uniforme mientras que sobre la componente e influye la aceleración de la gravedad, que hace que se frene el cuerpo (en el caso de que esté subiendo) hasta volver a acelerarse al descender y caer al suelo.

a = 0 – g

4.1.2 4.1.4 POSICIÓN: En la posición del objeto también intervienen las fórmulas de la posición del movimiento rectilíneo uniforme(sentido horizontal) y la posición del movimiento rectilíneo uniformemente acelerado (sentido vertical).

4.1.5 ALTURA MÁXIMA: En el movimiento parabólico, existe un punto (y sólo un punto) donde la partícula se encuentra en el punto más alto de su trayectoria.

En ese punto, la componente vertical de la velocidad es nula.

La fórmula para determinar la altura máxima no depende del tiempo.

A igual velocidad inicial y aceleración de la gravedad, la altura máxima de una trayectoria parabólica dependerá del ángulo θ de la velocidad inicial v₀.

La máxima altura que se puede alcanzar con una velocidad v₀ determinada se corresponde con un ángulo de lanzamiento θ = 90°.

4.1.3 4.1.6 ALCANCE HORIZONTAL MÁXIMO: La partícula o cuerpo llegará a su alcance horizontal máximo cuando caiga al suelo, es decir, cuando y sea cero. Podemos calcular el alcance sin saber el tiempo que ha tardado en recorrer la parábola la partícula o conociéndolo.

4.2 CONSERVACIÓN DE LA ENERGÍA

La ley de la conservación de la energía afirma que la cantidad total de energía en cualquier sistema físico aislado (sin interacción con ningún otro sistema) permanece invariable con el tiempo, aunque dicha energía puede transformarse en otra forma de energía. En resumen, la ley de la conservación de la energía afirma que la energía no puede crearse ni destruirse, solo puede cambiar de una forma a otra.

En el caso de la energía mecánica se puede concluir que, en ausencia de rozamientos y sin intervención de ningún trabajo externo, la suma de las energías cinética y potencial permanece constante. Este fenómeno se conoce con el nombre de Principio de conservación de la energía mecánica.

4.2.1 LA ENERGÍA: Es la capacidad de los cuerpos para realizar un trabajo y producir cambios en ellos mismos o en otros cuerpos. Es decir, la energía es la capacidad de hacer funcionar las cosas.

La unidad de medida que utilizamos para cuantificar la energía es el Joule (J).

4.2.2 ENERGÍA MECÁNICA: La energía mecánica es la suma de la energía cinética y la energía potencial de un cuerpo. Su fórmula es:

E _m = E _p + E _c

Donde E _m es la energía mecánica (J), E _p la energía potencial (J) y E _c la energía cinética (J).

La energía mecánica obedece al Principio de conservación de energía que estipula que “la energía no se crea ni se destruye, solo se transforma” por lo tanto se debe tener en cuenta las diferentes tipos de energía potencial que pueden existir en un cuerpo.

4.2.3 ENERGÍA CINÉTICA: Los cuerpos pueden realizar un trabajo por el hecho de estar en movimiento, es decir, los cuerpos en movimiento tienen energía. Esta forma de energía mecánica se llama energía cinética (E_C).

Cuando un cuerpo está en movimiento, tiene una cierta velocidad. Ya sabes que, para pasar del estado de reposo a movimiento, hay que aplicar una fuerza, que multiplicada por el desplazamiento del cuerpo es igual al trabajo que realiza.

4.1.4 ENERGÍA POTENCIAL GRAVITATORIA: Definimos la energía potencial gravitatoria como la energía que posee un cuerpo por el hecho de encontrarse bajo la acción de la gravedad. Su valor, para el caso de alturas pequeñas sobre la superficie terrestre, viene dado por:

Ep = mgh

Dónde:

Ep: Es la energía potencial del cuerpo. Su unidad de medida en el Sistema Internacional es el Julio (J)
m: Masa del cuerpo. Su unidad de medida en el Sistema Internacional es el Kilogramo (kg)
g: Valor de la aceleración que provoca la gravedad. Su unidad de medida en el Sistema Internacional es el metro por segundo al cuadrado (m/s²)
h: Altura a la que se encuentra el cuerpo. Su unidad de medida en el Sistema Internacional es el metro (m)

4.3 MOMENTO DE INERCIA

Es una medida de la rotacional de un cuerpo. Más concretamente el momento de inercia es una magnitud escalar que refleja la distribución de masas de un cuerpo o un sistema de partículas en rotación, respecto al eje de giro. El momento de inercia sólo depende de la geometría del cuerpo y de la posición del eje de giro; pero no depende de las fuerzas que intervienen en el movimiento.

4.4 VELOCIDAD ANGULAR

Es una medida de la velocidad de rotación. Se mide en radianes por segundo. Representada en el sentido de giro por , Donde v corresponde a la velocidad inicial y r al radio de giro.

4.5 TENSIÓN

La tensión (T) es la fuerza con que una cuerda o cable tenso tira de cualquier cuerpo unido a sus extremos. Cada tensión sigue la dirección del cable y el mismo sentido de la fuerza que lo tensa en el extremo contrario.

Por simplicidad, se suele suponer que las cuerdas tienen masa despreciable y son inextensibles (no se pueden deformar), esto implica que el valor de la tensión es idéntica en todos los puntos de la cuerda y por tanto, las tensiones que se ejercen sobre los cuerpos de ambos extremos de la cuerda son del mismo valor y dirección aunque de sentido contrario.